The Meaning of the 2015 PISA Canadian Math Results

For the past few years various news media have repeatedly conveyed the belief that:

1. The mathematical abilities of Albertan and Canadian students have declined significantly.
2. This decline was caused by the introduction of a new curriculum.
3. Evidence is provided by the results of the PISA tests.

That sentiment is what this post is about, but let me start with this question.

At a certain junior high school the averages of the math grades for the past three years were 73%, 75%, and 73%. How would you rate this school?

1. Definitely a top notch school.
2. That’s a pretty good school.
3. That’s what an average school should be like.
4. Mediocre — room for improvement.
5. Poor — I would think about sending my child to a different school.

Myself, I would choose (2).  I would expect grades of 65% - 70% to be about average so I feel the school is a pretty good one. Not absolutely fantastic, but pretty good.

The real story:

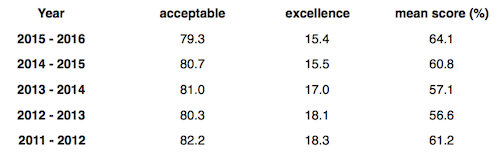
The averages cited above are not for a particular school, but for an entire country. The figures are the average math scores for top notch Singapore in the 2009, 2012, and 2015 rounds of the PISA tests. (If you are familiar with the PISA tests, you know that the scores are not recorded as percentages. The numbers 73%, 75%, and 73% are what you get when you convert the published PISA scores in a reasonable way.¹ )

For comparison, here are the Alberta and Canadian results for the years from 2003 through 2015, again converted to percentages. (Singapore did not compete prior to 2009).

The variation across the PISA rounds for all three regions seems pretty unexceptional. I would expect changes of ±3% at the very least — the year-to-year variability in my university math classes were at least as large as that.

[As an aside, I predicted in a previous post that Canada would get a grade in the range from 65% to 67% on the math part of the 2015 PISA test. I promised a Trumpian gloat if the prediction was correct, and a Clintonian sob if it was wrong. No guru here, I’m afraid — it was pure luck — but "Gloat. Gloat" anyway.]

In spite of the stable relationship between the results for Alberta and Canada, there is alarm that Alberta's performance in the 2015 round has pushed them below the rest of Canada. That may be numerically accurate when you look at the raw scores published by PISA, but the results are so close that when converted to percentages the difference vanishes. And, more importantly, the PISA consortium itself reports that the difference is so minuscule that it is not statistically significant. Which means there is no reliable evidence that there is any difference whatsoever.  

I don’t think that our ranking among the PISA participants indicates that our math curriculum is either superb or deficient. But using the PISA rankings to critique the curriculum is what people do. To confirm this, all you have to do is read the opening foray in the petition that stoked the current math wars in Alberta. Here is what it says:

"The Organization for Economic Co-operation and Development (OECD) recently released a report confirming that math scores, measured in 15yr olds, have declined significantly in the ten years since the new math curriculum was introduced across Canada."

Additionally, there is this report in the Globe and Mail in January 2014:

Robert Craigen, a University of Manitoba mathematics professor who advocates drilling basic math skills and algorithms, said Canada’s downward progression in the international rankings – slipping from sixth to 13th among participating countries since 2000 – coincides with the adoption of discovery learning.

So, what about that new curriculum?

The petition was presented to the Alberta legislature on Tuesday, Jan 28, 2014. (A later article gives a date of March 2014.)

So apparently the new curriculum was introduced a decade earlier, in 2004. However, that's not what happened — no students were taught the new curriculum prior to 2008 - 2009. To see just how far off the 2004 date is, let’s look at how the curriculum was actually phased in. Here is the schedule for the years that each grade was first exposed to the curriculum. (I trashed around a long time trying to find this. Thanks David Martin and John Scammell for providing me with the information. Since Albert Ed does not have this information on its website, I cannot be sure that Alberta actually followed the implementation schedule, but I'm assuming that was the case.)

The PISA exams take place every three years, and Canadian students take the tests in Grade 10. Just like David and John did in their 2014 posts², I’ll save you some time and do the math so you can see when the students were first exposed to the new curriculum. 

• Those who took the 2003 test - never exposed
• Those who took the 2006 test - never exposed
• Those who took the 2009 test - never exposed
• Those who took the 2012 test - first exposed in grade 7
• Those who took the 2015 test - first exposed in grade 4

The curriculum changes could not be reflected in any way by the PISA results prior to 2012. And those who wrote the PISA test in 2012 were not exposed to the new curriculum in the elementary grades (which is where those who blame the new curriculum for our decline are pointing their fingers).

The biggest drop in the PISA scores seems to have occurred in 2006, and the PISA grades since then have remained quite steady. What’s going on here?  Did the introduction of the new curriculum in 2008 cause a drop in the PISA results in 2006? Is this is a brand new type of quantum entanglement? As you all know, with ordinary everyday quantum entanglement, changes in physical properties can be transmitted across great distances instantaneously.³  Yes, instantaneously, but never backwards through time. As someone might say, that would be really spooky! 

Sorry for the sarcasm.

If you accept the PISA results as evidence of a decline of our students' math abilities, then those same results show that the decline occurred well before the new curriculum could have had any influence. And, this also means that the PISA results provide no evidence that returning to the previous curriculum will repair things.

Do the PISA scores matter?

By the way, if you are concerned about our sinking rank in the math PISA league tables, note that for the 2015 round, Canada moved up to 10th from the 13th place.

David Staples (a columnist for the Edmonton Journal) has said that the people who want to return to pre-2008 curriculum and teaching methods are not really concerned with our PISA rank (despite the comments quoted above). Their concern is that the proportion of lower performing students is increasing while the proportion of higher achieving students is decreasing.

Although that's true, and it might be serious, the decline started prior to 2015, when none of the students who took the PISA test were exposed to the new curriculum in elementary school. So, again, the PISA results are not evidence that the new curriculum is at fault. We'll have to go elsewhere to get evidence that it was caused by the new curriculum.

And if we can't find any, please let us not blame the front line workers and have this discussion degenerate into a round of teacher bashing.

---

REFERENCES

¹ The conversion from the published PISA scores to percentages was done as follows:

Percent_grade = 60 + (Pisa_Score − 482) × (10 / 62.3). 

More details can be found here .


² David Martin's post about the 2012 PISA round is here, and John Scammell's is here.

³ Quantum entanglement — I'll let others explain it. Here are two you tube videos that do a pretty good job.

Quantum Entanglement & Spooky Action at a Distance

Yro5 - Entanglement

** post was edited Dec 14 to correct two typos

Use it or Lose it !

This is not a column about sexual health.


I’m talking about the basic math facts — times tables and all that stuff that should be stored in our long term memory:

Will we really forget those facts if we don’t use them? 

Our brains are flexible. Neuroscientists use the word "plastic". They tell us that the brain's circuits can be repurposed, new ones can grow, and that frequent use strengthens neural connections. My guess is that YES, our memory of these basic facts will fade if we don't use them.


But I have a follow-up question.

Do you know that  1 / 1.04 = .96154? 

I do know that! And it's a fact that I don't use.


Here's the story.

Fifty years ago I worked for a large Canadian insurance company. I was a clerk in the mathematics section of the Policy Change department. My job was to compute how much to charge or refund when clients changed their insurance policies.

Among the many options available was the possibility of paying premiums in advance. The company liked it when clients did this, and to encourage them the company offered a discount.

We used an interest rate of 4%.  So, if the premium was, say, $150.00, and the payment was being made a year in advance, the client would pay $144.23, which is what you get from the following computation:

$150.00 / 1.04.

To the nearest five decimal places, 1/1.04 = 0.96154, so we could also calculate the discounted premium this way:

$150.00  ×  .96154.

Actually, 1/1.04 is slightly smaller than 0.96154, but for all practical purposes the two methods are identical. Yet, despite their equivalence, our boss made us use the second one. Instead of dividing by 1.04 we had to multiply by 0.96154. It was not because our boss had some weird mathematical fetish: an official company policy memo explicitly stated that when computing prepayments of premiums, we had to use the factors from the supplied interest tables. Policy trumps mathematics.

After a short time on the job, the "fact" that 1/1.04 equalled .96154 had established permanent residence in my mind and it still remains there even though I haven't used it for over half a century.

* * * * *

This sort of thing is not unusual.

• My parents-in-law, veterans of WWII, could recall their military ID numbers for their entire lives, even though they seldom used them.
  

• My wife and her mother used to play a game when she was a child. They recited the alphabet backwards as rapidly as they could. It's a skill that my wife has not used for over 60 years. Yet yesterday she showed me that she can still reel off the alphabet backwards without hesitation. 

So my intuition that facts fade from memory when they are not used may be wrong. Some of us retain basic facts and practiced skills even if we don't use them for an extremely long time.

* * * * *

On the other hand - 

Sometimes when people say "Use it or lose it" they really mean

Use it and you won't lose it!

Well, we all know that statement is false.

How else to account for my spotty recall of simple multiplication facts? I've used those basic multiplication facts quite a lot since leaving that insurance company, and I'm still not "fluent" with them. I can fire off the squares of the natural numbers up to 12 × 12, but ask me what 12 × 7  or 12 × 11 is and I have to perform a mental computation. And 13 × 13 is 169, but what is 13 × 9?

Some people can recall basic math facts quickly and without conscious effort — they automatically know them without thinking. Like the way I know that 1/1.04 is .96154.

Others will never completely achieve this type of fluency. When someone says "Twelve times seven" it may not provoke the involuntary "Eight-four". Instead, the reaction may be "seventy plus fourteen" having broken 12 × 7 into 10×7 plus 2×7.

To be truthful, I am fluent with most of the basic multiplication facts. But, I really do still have trouble with a few parts of the 6, 7, 8 and 12 times tables. And, as I prepared this post, I actually did have to retrieve 12×7 by that quick mental computation. However, once done, I could instantaneously recall the answer for the rest of the post, and I know that the automaticity will remain for several days, maybe even a couple of weeks. But it’s as impermanent as those facts acquired by cramming for an exam: very soon it will fade from my memory.

My advice 

If my children were young, this is what I would tell them today:

Practice your times tables. Memorize as much as you can. It is worth the effort. Maybe you will never be able to keep all of them in your head. But if you can keep a few there, and if you learn how to be flexible with numbers, you will find ways to derive the more difficult ones very quickly — almost as fast as if you had actually memorized them — and it won’t stop you from learning more mathematics.

As for getting every single one of those basic facts into genuine long term memory in a way that they can be instantly and automatically recalled: forget it — for me, and maybe for quite a few others:

It's • Not • Gonna • Happen

Addendum

Just as I was finishing this post, I came across an article (linked below) by Maria Konnikova in The New Yorker magazine. It's about the tenuous relationship between practice and achievement across a variety of fields (including mathematics). It's really worthwhile reading. 

Link: PRACTICE DOESN’T MAKE PERFECT

Understanding the PISA Tables

The PISA math results show Canada trending downwards internationally. Here are the rankings of the top 20 regions (of approximately 65) that participated in the 2003, 2006, 2009, and 2012 rounds:

Note:  Shanghai and Singapore have been greyed out for 2003 and 2006 because neither took part in those two rounds. Since it is hard to assess a trend when the population base changes, I think that either Shanghai and Singapore should be included for all rounds, or both should be excluded for all rounds. I have chosen to include them, and, based on their results in 2009 and 2012, I have assumed that they would have finished atop the PISA table had they competed in the earlier rounds.

With Shanghai and Singapore included, the perspective on the Canadian trend changes somewhat. However, some slippage is definitely happening, and for many people the trend is alarming.

But I wonder if we are concentrating too closely on the rankings. Here is the same table when grades are included:

Note: OK. This doesn't look like the PISA scores that you have seen. The results shown above are percentage grades, and the PISA consortium does not report the scores this way. Instead, they use a numerical scale that ranges from about 300 to over 600.

I have a fondness for percentage grades. They provide me with a more serviceable scale than grades out of 600. For example, to me, a class average of 67% indicates an ordinary but acceptable performance, while I am not sure what an average of 527 on the PISA scale conveys.

The conversion from the PISA scale to percentage grades in the table above was done linearly:

Percent_grade = 60 + (Pisa_Score − 482) × (10 / 62.3).

As is evident, Canada has remained remarkably stable: 68%, 67%, 67%, 66%. 

Proficiency Levels

The PISA results are intended to be a measure of mathematical proficiency, and PISA describes six different levels. The grade ranges for each level are as follows:

The descriptions above are extremely abbreviated. Detailed descriptions can be found in the 2012 PISA technical report (link [5] below). Also, PISA does not use verbal descriptions like Highly proficient or Basic proficiency.

Some features of the PISA proficiency levels

• For each round, the PISA consortium adjusts the grades so that the proficiency levels retain the same meaning over the years. A percentage score of 65% in 2003 has exactly the same meaning as a percentage score of 65% in 2012. In other words, PISA takes care to avoid grade inflation.

• On the percentage scale, each Level band is 10 points wide. On the PISA scale, the bands are 62.3 points wide.

• The PISA scales are designed so that the OECD mean is 500 (or very close to 500). On the percentage scale, the OECD mean is 63%.

• Over the four rounds from 2003 to 2012, Level 6 has never been achieved by any of the participating regions. Level 5 has been achieved by one participant. Level 4 has been achieved by five participants.  In the four rounds from 2003 to 2012, Canada has resided in the Level 3 band.

Is the slippage significant?

The difference between Canada’s score in 2003 and 2012 is statistically significant. The words mean that, with high probability, the difference in the scores is real and is not a result of the chance that arises by testing only a sample of the population. Statistical significance tells us that the statistics are reliable, but it doesn't tell us anything about whether or not the statistics are important.

(The word "significant" has considerable emotional impact. I remember a Statistics professor telling us that the word should be outlawed when we are discussing statistical results.)

Do the differences in the PISA tables show that Canada must do something to improve how our students learn mathematics? Some people believe that the statistically significant difference between 2003 and 2012 is also of great practical significance, and they have strong opinions about what should be done.

As well, the PISA group itself has investigated what will and won't work to improve students mathematical proficiency, and has published its findings in a 96 page document [6]. Some of the conclusions appear to run counter to what the back-to-basics people advocate — one conclusion in the document is that dependence on intensive memorization and rote practice of the basic algorithms is a poor strategy for learning anything but the most trivial mathematics.

That particular PISA document may leave some of my friends in a slightly awkward place: Those who have used the PISA tables as a rallying cry for a return to traditional methods now find themselves having to rebut some of PISA's own conclusions about what constitutes good teaching and good curriculum.

In any event, when I look at the percentages for Canada from 2003 to 2012, I see changes, but I don't think that they are earth-shattering. Would you be concerned if one section of your Calculus course averaged 68% and another section averaged 66%? I’ve run into that situation teaching back-to-back sections of the same course, and I was not convinced that the section with the higher score was the superior one.

* * *

In a few weeks, the OECD will release the results of the 2015 PISA round. I am very interested in seeing if Canada's results are significantly different in a practical sense. My expectation (based on no evidence whatsoever) is that the results will be much the same as before, and will fall within the 65% to 67% range. ( Hey! A Halifax weatherman had a very successful forecasting run by predicting tomorrow's weather to be the same as today's.)  I'll do a Trumpian gloat if my prediction is correct, and a Clintonian sob if it's wrong.

References

[1] 2003 PISA report (Math scores are on page 92)

[2] 2006 PISA report (Math scores are on page 53)

[3] 2009 PISA report (Math scores are on page 134)

[4] 2012 PISA report (Math scores are on page 5)

[5] PISA 2012 Technical report (Proficiency levels are described on pages 297 - 301)

[6] Ten Questions for Mathematics Teachers… and How PISA Can Help Answer Them, OECD Publishing, Paris (2016).

Alberta's new math curriculum

Will David Eggen be prudent in his redesign of the K-6 Alberta math curriculum?

A few days ago, the Provincial Achievement Test results were released, and the media reacted:

Math scores dip as Alberta Education releases latest PAT results
— Metro News, Oct 7

Calgary students show well on Alberta PAT tests, but concerns over math scores
— Calgary Sun, Oct 8

Math results continue to slide on Alberta provincial exams
— Edmonton Journal, Oct 8

Grade 6 math marks concern Edmonton school boards, Alberta education minister
— Global News, Oct 7

Province and schools eye changes as grade six math students struggle
— CHED, Oct 8

So what are the results?

Here are the percentages of students that achieved acceptable and excellence status in the Grade 6 math PAT’s from 2011/12 to 2015/16 (the data is from the Alberta Education website):

The bandaid solution?

Already some curriculum changes have been made. Recent amendments include memorization of the addition and multiplication tables and learning the standard/traditional algorithms. The format of the algorithms is not explicitly specified. This means, for example, that any of the following three would qualify as the standard division algorithm:

Where did these come from? The leftmost algorithm is the one I was taught umpteen years ago. The other two are the ones my grandsons learned a few years ago during the midst of the math wars. I don’t know if any of these were being taught in elementary schools throughout Alberta. I presume not, otherwise there would be little need for the Summary of Clarifications published here. (Alberta Education does provide a very simple example of a division algorithm. It resembles the one I learned as a youngster — one which I did not really understand at the time.)

A brand new wrinkle in the curriculum is that the Math 6 PAT's will now have a no-calculators-allowed part: 

Part A [of the PAT] is a 15-question test including five multiplication/division questions, five "connecting experiences" questions, and five "number relationship" questions, according to a guide for testers. Calculators are not permitted, and the test is designed to be finished in 15 minutes. 

— Edmonton Journal, Sep 1.

Some people have said that the time pressure created by this part of the test helps prepare the students for the pressure they will have in the real world. (Whose real world is that? Mine? The teacher’s? Part of education is to help students understand their real world, which is radically different from an adult's real world. I think that a child's real world provides plenty of pressure without a timed test.)

Do the PAT scores mean that more changes are needed?

Without knowing how the cut points for the PAT tables are determined, and without knowing why the average test scores are increasing while the percentage of successful students is decreasing, it is difficult to tell if the PAT results indicate that more curriculum changes are needed.

I'm not sure that the PAT results even matter — everyone knows that the real driver for curriculum change is the belief that we must get higher scores on international assessments like PISA. However, as signalled by the media headlines, the grade 6 PAT scores will surely be used to apply more pressure to David Eggen's real world.

A final thought

Currently I'm involved in preparing material that ties our math fair puzzles to the Alberta K-6 mathematics curriculum and to the American Common Core State Standards for K-8 mathematics.

By necessity, I have spent quite a bit of time examining the Alberta K-6 part of the curriculum. It is based upon four mathematical strands and seven overarching mathematical processes which together provide ample mathematical proficiency. I don't think that wholesale rejigging is needed. I feel that the curriculum as it stands already encourages the growth of mathematical thought along with practice and understanding of the basic numeracy skills. I hope this balance will not be upended by the new curriculum.

Three simple ordinal number puzzles

There are two fundamentally different ways that we understand numbers, namely as cardinals and ordinals. When we think of a number as magnitude or size, that's a cardinal number. When order and sequence are the things we want, then we are dealing with ordinal numbers.

In a previous post I related how I handle ordinal numbers more easily than ordered sequences of other things (like the English alphabet). I thought it might be interesting to create a couple of puzzles that deal with ordinal numbers.

Here are three puzzles that are intended for children in the elementary grades, but they can be scaled up to higher levels. The first two are quite new (but I recently discovered a version of the first one in Kordemsky's "Moscow Puzzles".  The third puzzle is one from a small set that I made up over 15 years ago.

Each puzzle asks you to rearrange a set of numbered disks (or tiles) so that they are in numerical order. What makes the puzzles a challenge is that there are restrictions on how you can move the disks.

Swap positions 1

For this puzzle you require five disks numbered 1 though 5. Place them in a line in random order:

The puzzle is to rearrange the numbers so that they are in order:

You cannot just rearrange them any way you want.

Rules:

• You must solve the puzzle in a step by step fashion.
• For each step you must swap the positions of two numbers.

Here are two possible steps for the puzzle above. (Not saying that these steps are part of the solution.)

You always have to swap two numbers. You are not allowed to squeeze one number between two others like this:

Small Spoiler:  (Use your mouse to select the hidden text in the following box.)

With these rules, the solver may soon figure out that you can swap two numbers that are next to each other and successively move a number up and down the line (thereby inventing an algorithm that solves the puzzle).

Swap Positions 2

Let's adjust the rules and make it just a bit more difficult. And because it is more challenging, try it using four numbers instead of five.

New Rules:

• You must solve the puzzle in a step by step fashion.
• For each step you must swap the positions of two numbers.
• The two numbers must have at least one other number between them.

This is what you can and cannot do under the new rules:

Some other modifications are suggested at the end of this post.

The criss-cross puzzle

For this puzzle you will need a grid of squares forming a cross, and three tiles numbered 1, 2, 3 that will fit in the squares of the grid:

Place the tiles in the grid in the order 3-2-1 from left to right. By pushing the tiles within the grid, rearrange them so that they are ordered 1-2-3 from left to right. The tiles must end up in the position shown.

Rules:

• The tiles must always move and stay inside the grid.
• You can push tiles up, down, left, or right as long as you stay inside the grid. You cannot push a tile past, or over, or under another tile.
• If two or more tiles are touching you can push them together at the same time. 
• You cannot separate tiles that are touching by pulling them apart in the same line.

This move is OK. Here, the three tiles have together been pushed to the left.







This move is OK. You can push a tile up or down as long as it stays inside the grid.







But this move is Not OK. You are not allowed to pull tiles apart in the same line if they are touching.





You can also try the puzzle with different starting positions:

Note:  Depending upon the student(s), you might want to prepare them for the puzzle by letting them get familiar with moving the tiles. For example, have them figure out how to solve the following puzzle which only asks them to switch the position of the red tile. It's an interesting puzzle in its own right. The rules for moving the tiles are the same.

Possible modifications

Both swap positions puzzles can be solved for any set of numbers, e.g.,

What if we change the rules so that you are only allowed to swap numbers if they have at least two numbers between them? What other modifications could you make for the puzzle?

You can extend the criss-cross puzzle (to include more tiles) by changing the playing board. Here are two possibilities. The rules remain the same.

Computer science students: Can you write a program that solves these puzzles?

The curious incident of the mathematician at the self-checkout kiosk

We had some produce that had no barcode on the package, so we tapped the [ LOOK UP ITEM ] rectangle on the touch-screen, and it displayed some options for identifying the product:

The product did not have a 4-number code, so the choice was to search for the product alphabetically. For example, if the product was beans you would touch the B - C button which would bring up an array of pictures — Bananas, Basil, Beans (green), Beans (wax), Bread, Brussel Sprouts, etc. (Of course, touching one of these might lead to yet another screen, and so on until you see the exact item you wish to purchase.)

The actual product we wanted was grapes. So indulge me: what button would you touch?

At the kiosk I noticed that there was some hesitation when my wife responded. I wondered if it might be different if she had to choose a number range instead of a letter range. So we both did a quick trial when we got home.

The at-home kiosk task

On the right is a search screen that uses numbers instead of letters.

Here, the problem is to choose the button with the number range that contains the desired number.

Which button would you touch for the number 7?

These is very much the same question with numbers instead of letters. So, why were we able to answer this question much more quickly using numbers? 

Perhaps it is because I have had more practice with numbers — I am a mathematician, after all. But that doesn’t explain why my wife had the same experience — she is not a mathematician — and she also answered more quickly when numbers were used.

When I was a child, we spent a lot of class time learning how to find a word in a dictionary. We learned how to bracket words alphabetically —  and we learned how to put things in order alphabetically, and the teacher made sure we had lots of practice.  We knew the order of the English Alphabet quite intimately. What we did in school was a much more demanding task than selecting the correct screen at a checkout kiosk.

If you have read my previous post (It’s not all snake oil) you know that I have some interest in understanding how the brain (and mind) reacts to numbers.

That post was concerned with cardinal numbers — numbers being used to describe magnitude or size. It is now well established that there is a specialized region of the cortex that reacts to such numbers, and the region seems to be unresponsive to things other than numbers (such as colours, or music, or words that are not tied to numbers).

In the at-home kiosk task, however, we are dealing with ordinal numbers — numbers being used to describe order and sequence.

Recently, cognitive neuroscientists have begun more closely investigating both ordinal numbers and more general (non-numerical) ordered sequences. But the state of affairs is not clear cut. Exactly what happens depends on a large variety of factors.

Even the situation regarding ordinal numbers by themselves appears to be clouded by the fact that numbers represent both magnitude and order. When you are asked "Is 7 between 4 and 11?" do you decide this "immediately" in some sort of a subitizing way, or do you decide by comparing the magnitude of 7 successively to the magnitudes of 4 and 11? The answer seems to be that it depends upon the context, and that affects what regions of the brain are involved.

In particular, I was curious to see if there was a distinction between how the brain deals with the ordered sequence of numbers as opposed to the ordered sequence of the alphabet.

From what I have read the only conclusion I can draw is  "Maybe."

For now, I guess I'll  have to live with the fact that my wife and I are alphabetically challenged.

It's not all snake oil

If you are a teacher, what do you think about the following (real life) situation? 

Teacher: "It’s 1 o’clock. Today, school ends at 3 o’clock. How long do you have to wait?"
Student: "Two hours."
Teacher: "What’s 3 minus 1?"
Student: (After considerable struggle, cannot answer.)

—

Teacher: "What’s 4 divided by 2?"
Student:  Cannot do this, but announces the fact "Four times three is twelve."
Teacher: "Here’s four marbles for you to share among two students."
Student:  Without hesitation, separates the marbles so that he holds two in each hand.


The interaction described above is an abridged version of an account related by Stanislas Dehaene in his book "The Number Sense." (Links provided below.)

Stanislas Dehaene is a cognitive neuroscientist with a strong background in math and computer science. The student is M, is one of his patients. M is not a child, but is a retired and talented artist who has a brain lesion in the inferior parietal lobe of his brain.

Mr. M has some knowledge of numbers. He knows the history of certain numbers and can give lengthy lectures about the significance of some historical dates.  In his mind, he can move back and forth among the hours of the day. He is sporadically successful when dealing with numbers in other very concrete settings. He has some rote verbal memory and can recite such things as "Three times four is twelve," but he has no comprehension of what that means. He has absolutely no understanding of numbers when they are presented as abstract quantities. Despite considerable effort, Dehaene has been unable to teach M how to do even the most simple arithmetic computations in an abstract setting.

For a platonist like me, numbers exist independent of my own mind. They have meaning without any concrete context whatsoever. Five plus four is always nine, whether it is five apples plus four apples, or five cars plus four cars, or five miles plus four miles. The concrete setting — apples, cars, or miles — has nothing to do with what 5 + 4 is.  Five plus four is nine, and that’s it. It has meaning all by itself. It is one of the ultimate permanent properties of number.

But Mr. M shows us that, whether or not numbers are real things, the platonist’s concept of numbers as abstract entities is not independent of one’s brain. For Mr. M, such numbers do not exist.


Dehaene’s book is an account up to 2011 of what cognitive psychology and neuroscience has revealed about number sense and how we create it. Much of this is made possible by advances in brain imaging techniques that provide highly detailed pictures of the functioning of the brain (see the notes at the end of this post).

Thousands of studies have shown that the adult brain has an intricate network of neural circuits that react to numbers. The studies show that numerical undertakings activate localized regions throughout the cortex, and that these regions are found in the basically the same physical location in every brain.

One fairly specific region that reacts to numbers is located at the back of the brain in the groove between the two hemispheres. It is called the HIPS region (short for the horizontal part of the intraparietal sulcus). It seems to be almost exclusively devoted to number size and magnitude. In other words, it is one of the regions that reacts to cardinality — to numbers as quantity as opposed to numbers representing order or sequence.

The HIPS region doesn't appear to react to anything other than numbers. And it reacts no matter what mode is used to input them — spoken words, printed Arabic numerals, collections of dots. You cannot even sneak a number into the brain without activating that area. It reacts to numbers even if you are not consciously aware of them — the briefest subliminal exposure of an Arabic numeral hidden amongst a stream of other visual stimuli activates the HIPS region while the same stream without the numeral has no effect.

It's satisfying to discover that a certain part of the brain is tuned to a notion so fundamental as cardinality. But there are some surprises: the relationship between the activity in the HIPS region and cardinality is not so neatly packaged as one might hope.

To illustrate the complexity, take a few seconds to solve the following simple puzzles. In each puzzle, you have to place the correct symbol, either = , or < , or > ,  in the square to make the math correct. As usual, the symbol < means "less than," while > means "greater than."

The puzzles are not very challenging. But did you attend to the length of time it took you to solve them?  Here is what I think happened:

Puzzle A: You solved it instantaneously.
Puzzle B: You solved it quickly, but you performed a brief double check.
Puzzle C: You counted the dots in some manner (or you just skipped this puzzle altogether).
Puzzle D: You solved it instantaneously.
Puzzle E: You counted the dots.


The speed with which you solved these puzzles echoes the activity in the HIPS region, and the correlation is quite strong. The greater the activity in the HIPS region the quicker you will have solved the puzzle.

What is happening is this: when you are presented with two numbers that are small and different (puzzle A) or numbers are large and fairly far apart (puzzle D), there is strong activity in the HIPS region. For numbers that are close in magnitude, the activity in the HIPS region diminishes as the numbers get larger (puzzles C, and E, and even B to some extent).

What you have just experienced is three separate ways that we compare magnitudes. As adults, we typically do it by counting to obtain the exact magnitude, but that is not the only way.

We solve puzzle D without actually knowing the exact magnitudes. Cognitive neuroscientists call this the approximate number sense and describe the quantities as analogue magnitudes. They use a pan balance (an analog device) to model what is happening.  A pan balance can readily distinguish between, say, a collection of 60 one-gram tokens and a collection of 80 one-gram tokens without knowing the actual number of tokens in each collection. However, when comparing 60 tokens with 59 tokens, the pan balance cannot so easily distinguish the difference, just as the HIPS activation is weak when two large numbers are close in magnitude.

Puzzle A illustrates yet a third way that we compare magnitudes. Small numbers seem to have a special treatment by our brains. Although you may think that you just rapidly counted the dots, it is unlikely that you really did. Psychologists refer to the ability to accurately estimate small quantities without counting as subitizing.

Young children can subitize the difference between 1, 2, or 3 objects. Many animals also have this ability, and both children and some animals have an approximate number sense. What young children do not have, and what animals do not have, is the adult human’s precise sense of cardinality. Older children acquire it but animals never do. Humans can eventually learn to compare magnitudes of virtually any size — we learn how to count, and we learn what counting means. This is a number sense that we are not born with — it is a cultural artifact — we acquire it through education provided by our parents and teachers.

If we are given a bag of marbles and we count them 1, 2, and so on, until we reach the last marble with a count of 31, then we learn that 31 represents precisely the quantity of marbles in the bag. We learn that every bag of marbles has a precise quantity associated with it. And if for a second bag the last number reached turns out to be 34, we know that second bag has more marbles than the first one.

Tribes or groups of humans that do not count, or that only have a very rudimentary numbering system, cannot discern the difference between even moderate quantities when the quantities are close in magnitude. For such people, there is absolutely no difference between a bag of 31 marbles and a bag of 34 marbles.

Don’t you find this intriguing? One of the foundational aspects of mathematics, the notion of a precise cardinality, is a human creation.

Some additional notes

Brain imaging

In the past two decades new brain imaging techniques such as fMRI (functional magnetic resonance imaging) and MEG (Magnetoencephalography) have been developed that allow the brain to be studied in great detail. These techniques examine the functioning of the brain, not just the anatomy. With fMRI it is possible to scan activity across the entire cortex with a spatial granularity of 1 to 6 millimetres. With MEG we can monitor duration and response times with a resolution in the order of milliseconds. These techniques are noninvasive and hundreds of images can be gathered in a few minutes without danger to the people and patients who have graciously allowed researchers to test them.

The distance effect  

When numbers are large but close together, it is difficult to discern a difference between them. This is called the distance effect.  For puzzles A through E above, using dots enhances this effect, but brain scans and psychological studies show that the distance effect remains even when numbers are presented using Arabic numerals. It takes a bit longer to decide which of 18 or 19 is larger than it does to decide which of 4 or 5 is larger.

Ordinal numbers

As well as using numbers to describe quantity, we also use numbers to describe order. When we want to distinguish between the two different uses we typically refer to them as cardinal numbers and ordinal numbers.

As children learn to count, they are also acquiring an ordinal number sense. When a child counts "1, 2, 3, 4,"  she must understand that order is important, that 1 is always before 2 which is always before 3 which is always before 4.

Brain imaging studies have been used to explore how the brain reacts to ordinal numbers. Instead of asking "Which of these two numbers is the larger?" the question becomes "Are these three numbers in order?"  In one study, the ordering question was presented both symbolically using Arabic numerals, and nonsymbolically using dots.  With Arabic numerals, the brain regions that are are activated for the ordinality task are separate from the regions that are activated for the cardinality task. With nonsymbolic representations, there is considerable overlap.

Implications about education

Education strategies based on cognitive psychology are often viewed as some sort of snake oil. Indeed, I react somewhat negatively when I see phrases like "brain based teaching methods."

But current research, which combines "hard" neuroscience with "soft" psychology, seems to be very solid, There are already important conclusions about how we acquire number comprehension, and I expect that as the science progresses, we will have to rejig current theories about learning.

For example, we now know that children are born with neural circuits that can be adapted for number comprehension, and that they are ready for such accommodations quite early. The research show that infants have an approximate number sense and can subitize small numbers. And contrary to the widely accepted belief about "object impermanence," young children do not think that objects cease to exist when they are out of sight. In other words, children are ready to begin acquiring arithmetical concepts much earlier than prescribed by Piaget’s constructivism.

Another result, perhaps more disturbing, is that recent fMRI studies indicate that not all brains are tuned with the same acuity (thereby raising the spectre that there is such a thing as "math brain").  It is not known whether the differences are due to nurture (practice and training) or nature (biological). The current hypothesis is that it is due to both.

The new cognitive neuroscience does not have all the answers, and there is danger of being too optimistic about what it offers. But it tells us that we should paste handle with care labels on our lesson plans.

Links etc.

Stanislas Dehaene, The Number Sense [How the mind creates mathematics], revised and expanded edition, Oxford University Press, 2011. 

Here are two related online videos by Stanislas Dehaene. The first is an 8 minute interview (French with English subtitles). The second one is long and in French and covers the material in his book.

Where do mathematical intuitions come from?

La bosse des maths 

The following 30 minute video (in English) shows the detail possible with modern brain imaging techniques. Although it is about reading rather than math, it is what led me to buy Dehaene’s book about the number sense. 

2012 WISE Summit Focus

A letter to my cousin

Hi Barb,

Thanks for the link.

I have thought a lot about this controversy (the Canadian Math Wars). It’s a horrible state of affairs, and it should stop.

I'm afraid that I'm going to have to play "Blame the messenger," because articles like this one
pit the general public and some academics against the teachers and our education systems. I think the fault lies with the laziness of news columnists who reflexively go to the easiest sources. Whenever something is written about math education in Canada you can almost guarantee that the most prominent position in the article will be given to Robert Craigen or Anna Stokke deriding the current state of affairs. Controversy sells newspapers and TV programs.

In my opinion, the math wars stem from two things. First, new students entering university are ill-prepared for their math courses (upsetting the math profs because the students do not know the fundamentals). Second, teaching methods have changed since the students' parents went to school (upsetting the parents because they cannot help their children with their homework).

This gives rise to the sentiment that math education was better in the past, and that it is currently in decline. This is bolstered by the fact that Canada’s scores are slipping in international math tests such as PISA. [ PISA = Programme for International Student Assessment. ] The result is a desire to go "back-to-basics" and to confine teaching to the "traditional" ways.

Here is my take:

When I first started teaching at U of A forty years ago, I also found the students to be ill-prepared, so this is not a new perception.

It is true that changes have been made in the way math is being taught, but I don't think it's a bad thing. Just ask a few of your friends about how they did in math at school. I’ll wager almost every one of them will say "I was no good at it!" In other words, we were pretty bad at teaching math in the past, so changes in our teaching methods had to be made. And I cannot understand why someone who says they are bad at math would want things to revert to the way they were taught.

As far as PISA goes, I have doubts that the results are a reliable measure of math education. But even if they are, I don't think we have slipped that much. Canada is still among the better performing countries. Finland is perennially cited as one of the best, and in the 2012 PISA round of tests, Canada was merely one step below Finland. Incidentally, Pasi Sahlberg, a highly respected Finnish educator, recently tweeted "The world needs more Canada."

And by the way, newspaper columnists almost always use the term "discovery math" when talking about some of the more up-to-date teaching methods. It's a very loosey-goosey term that implies that current teaching methods forbid direct or explicit instruction thereby leaving students to flounder helplessly on their own.

I don't believe that this is really happening, especially the part about forbidding direct/explicit instruction. In the past three years I must have read hundreds of blog posts by teachers describing how they taught one or another topic in mathematics. Most of them presented thoughtful routes through the lesson. They all involved direct or explicit instruction at some point, 'though not the way you and I experienced it. 

I guess I can sum up my feelings this way:

I agree that there is room and need for improvement in our math education, and I have opinions about that, but "Forward To The Past" should not be an option.

Regards,

Ted

PS. Somewhat off-topic: A few years ago, the doll with your namesake caused quite a stir when it was programmed to say "Math is hard!" A school teacher told me Barbie should have said: "Math is hard, and teaching math is even harder."

PPS. You can read about my biases against PISA here and here.

Math and History - a comparison of two subjects

History
My grades were not good. They were "consolation" grades — the sort of grades that say: "You showed up for the exam and spelled your name correctly so I’m giving you a pass in the course."

I did not develop a sense of epoch. I had trouble grasping the significance of major historical events. Our history books and lessons were an unitemized list of facts, dates, and names. Wars and revolutions happened, and then they ended, and that was it. There was no connective tissue. There was no pattern. History was a confusing and uninviting subject.

Mathematics
In high school, I liked math and I was "good" at it. My grades were excellent.

My brush with Arithmetic in elementary school was disagreeable. However, in high school computational skills were not front and centre, and I got along extremely well without them.
My Algebra and Geometry and Trigonometry courses made sense. There were clear bonds between them. There was a sense of inevitability as we worked through the material.

 * * * 

Of course, the description of my History courses is not accurate, but that’s how I reacted to them. So I ask: 

What sucked the joy out of my History courses? 

I do not know the answer.

Now go back to the first two paragraphs of this post and replace the word History with the word Mathematics. Does this describe how some students feel about math?

So what sucked the joy out of their Mathematics courses? 

I don’t know the answer to that question either.

How did you learn your times tables?

When I was a kid, I liked playing ice hockey. I was actually not very good at it — no Connor McDavid here!  But I did acquire the basic skills. For example, I figured out how to lift the puck. (For you non-hockey players, that means shooting the puck in such a way that it flies off the ice into the air. It’s a essential skill if you want to be able to score goals.)

I practiced that skill a lot. Whatever I did, it worked. I could lift the puck consistently without thinking about it. I haven’t shot a puck for many decades, but whenever I imagine doing so, I swear can feel the memory in my triceps.

Of course, I really did not "figure out" how to lift the puck. I did not know the theory behind the lifting action. And to the extent that the skill was necessary, I didn’t need to understand the theory.

The lesson is this:

When learning something new that you will need for later use, master the mechanics first. You can learn why it works later.

* * * Warning: possible straw man ahead * * * 

It’s a useful lesson.  It helps me understand the approach to mathematics teaching advocated by the back-to-basics people: You can be successful by learning the how without understanding the why. Just learn the essential basic facts and algorithms. Don’t worry about why the puck flies into the air — just practice shooting enough so that you can lift it consistently and effortlessly.

Reasonable advice? Maybe. But, no matter how hard I practiced, I could not always "lift" the multiplication tables. As far as the basic multiplication facts are concerned, I do not have what some people call rote recall — I do not have the ability to rapidly and effortlessly retrieve all of the basic learned facts from memory.

A great chunk of my own elementary math education was founded on the contrary belief, that rote recall is, in fact, achievable by everyone — that all it takes is practice.  Accordingly, my classmates and I were regularly drilled and tested on the multiplication tables. I did not do well, and I argued with my teachers. Ultimately, I was punished for my inability to memorize the 12 x tables.

I don’t believe that my recall difficulties are exceptional. The more blogs I read, the more I suspect that there are many people who, no matter how much they practice, will never possess rote recall of the basic arithmetic facts. In that sense, those people can never know the basic facts.

So, it was with interest that I read that Nikki Morgan, the secretary of state for education in the UK, has decreed that:

"we are introducing a new check to ensure all pupils know their times tables by age 11"

An interesting post by @thatboycanteach asks what it means to "know" the times tables. Like me, he suffers from what might be described as rote recall deficiency. And like me, he survived (and even thrived) by using various work-arounds to compensate.

The UK times-table test will be computerized and time-restricted. It looks like it will be based on pure rote recall. For the flunkies, there will undoubtedly be some sort of penalty. It’s unlikely that they will be physically punished like I was, but even non-corporeal punishment can inflict great stress and harm and, in the end, may prevent them from learning mathematics.

What is of concern to me in Alberta is that, however sincere the back-to-basics people may be, they seem to be basing their reform efforts on the very thing that caused me difficulties, namely, the belief that all students can and must achieve rote recall, that this is the only way to know the basic facts.

That is the conclusion that I draw from reading their petitions and press releases. If I’m wrong, if I am raising a straw man, it is difficult to understand why they also want to banish the teaching of alternate approaches to the basic facts and algorithms that are needed so that people like me can compensate for our deficiencies.

Math fair workshop at Banff

The 14th annual math fair workshop at BIRS will take place over the weekend of May 6/7/8, 2016.
(BIRS = the Banff International Research Station.)

Right off, let me say that I have a pretty bad attitude about school science fairs.  You know — those competitions with poster sessions, baking soda volcanoes, and parent-created displays. The ones that end with an obligatory showcasing of a winner — a bright student who looks like he/she will go on to become the next Neil deGrasse Tyson, and who, for a short while, will be a poster-person for our education system.

OK, that's harsh, but it is still very much the norm to single out a winner.

How about having one that does not overly favour the highly talented? One that even a less confident student would enjoy and not end up feeling like a failure because he or she did not win a medal.

If you’re like me, you do not enjoy being tagged as a loser, and you would likely withdraw from a situation where that is liable to occur. Aviva Dunsiger touched upon this in her blog. Although her post is about phys-ed rather than mathematics, she paints a clear picture of the response to anticipated failure:

Yes, there were always strong athletes, but those that struggled (and I was one of them) wanted nothing to do with phys-ed. With my visual spatial difficulties, games like volleyball, basketball, and baseball were a tremendous struggle. I certainly never got picked for a team, and I couldn’t blame anyone. Why would I want to be physically active if I was only going to meet with failure?

[the emphasis is Aviva's]

Can we have a math fair where students can be mathematically active without the anticipation of failure?  One where students do not need a badge or ribbon to confirm that their efforts have paid off ?

Such math fairs do exist. They’re called SNAP math fairs because they are Student-centred, Non-competitive, All-inclusive, and Problem-based.

The fairs are built around math-based puzzles. The students first solve the puzzles^[1] and afterwards prepare the artwork and puzzle pieces that are required to display them.  

Visit such a fair and you will find students manning their puzzles. But, you will not see them exhibiting the solutions. Instead, they will invite you to try the puzzles yourself, and they will give you hints and help when you run into difficulty. The math fair is very interactive. It is much more than a poster-session.

* * *

Here are a couple of puzzles from past math fairs. The first one is for younger students to solve. 

Cats Pigs and Cows

A farmer has nine animal pens arranged in three rows of three. 

Each pen must contain a cat, a pig, or a cow. 

There is already a pig and a cat in two of the pens. 

The farmer wants you to fill the remaining pens so that no row or column contains two of the same animal.

The second puzzle is for older students.^[2]

The Sword of Knowledge

The dragon of ignorance has three heads and three tails. 

You can slay it with the sword of knowledge by chopping off all of its heads and all of its tails. 

With one stroke of the sword, you can chop off either one head, two heads, one tail, or two tails.

But the dragon is hard to slay !! 

• If you chop off one head, a new one grows in its place. 
• If you chop off one tail, two new tails replace it. 
• If you chop off two tails, one new head grows. 
• If you chop off two heads,  nothing grows.

Show how to slay the dragon of ignorance.

* * *

A SNAP math fair is remarkably adaptable to many different circumstances. If you are interested in learning about how you can incorporate a SNAP math fair into your own teaching environment, come to the BIRS workshop. You will meet teachers who have organized math fairs in their own schools. You will also meet a few mathematicians who have taught courses in which a math fair was key ingredient. 

As well, there will be math fair resources available, and the participants will be involved in puzzle-solving sessions.  

The BIRS workshop has room for about 20 participants, and it is oriented towards (but not limited to) K-9 teachers.

For more details about SNAP math fairs, visit the SNAP math fair site. And while you are there, take a look at the Gallery to see how students react.

For more information about the workshop, and who to contact, the link is here.

End notes

^[1] The solving part is a crucial element of the math fair.  Ideally, students solve the puzzle by themselves. They are surprisingly persistent.

^[2] I imagine the Sword of Knowledge puzzle would work with junior high or high school students. However, I once visited a SNAP math fair where two grade five students had solved it. Their teacher told me that they struggled with the problem but solved it after one of them grabbed a handful of pencils (tails) and erasers (heads).