The workshop is all about how to run a math fair that emphasizes puzzle solving with lots of interaction between the math fair visitors and the student presenters. The workshop participants will primarily be teachers, including some who have organized highly successful math fairs in their schools. More details about the workshop can be found here. I hope you will consider coming.
 |
| Some of the participants at the April 2017 workshop |
The workshop sessions are held in the TransCanada Pipelines Pavilion. It's a superb venue, with the all the capabilities and facilities you would expect from a leading research institution.
 |
| TransCanada Pipelines Pavilion. Photo Courtesy of The Banff Centre. |
–––––
Here are some examples of the sort of puzzles that we will be working with. These happen to involve arithmetic operations, but that is not obligatory –– all that is required is that the puzzles be mathematically based.
Fill in the digits

| 
|
|---|---|
| (a) | (b) |
 |
(c) |
(a) Put the digits 1, 2, 3, and 4 into the squares to make a correct sum. Use all four digits.
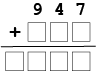
(b) Put the digits 1, 3, 6, and 8 into the squares to make a correct sum. Use all four digits.
(c) Put the digits 1 through 7 into the squares to make a correct sum. Use all seven digits.
(c) Put the digits 1 through 7 into the squares to make a correct sum. Use all seven digits.
The following two examples are both based on the same idea and show how puzzles can be adapted to challenge students at different levels.
Crosses and Sums


In the cross above, the numbers from 9 through 12 have been placed in the squares in such a way that horizontal and vertical sums are the same.
( 10 + 8 + 11 = 9 + 8 + 12. )
In each of the crosses below, the squares have to be filled with all of the digits from 1 through 5.

|

|

|
|---|---|---|
| (a) | (b) | (c) |
In each of (a), (b), and (c) put the remaining digits from 1, 2, 3, 4, 5 into the empty squares to make the horizontal and vertical sums the same.
Spokes
In the following figure, the digits from 1 through 7 have been placed in the circles so that the sums along the lines are the same:
1 + 7 + 6 = 2 + 7 + 5 = 4 + 7 + 3.

In each of the following, the circles have to be filled with the digits from 1 through 7. In each case, three of the circles have already been filled.
 |
(a) |
 |
(b) |
(a) Place the numbers 1, 2, 3, and 7 in the circles so that the sums along the lines are the same.
(b) Place the numbers 4, 5, 6, and 7 in the circles so that the sums along the lines are the same.
Both the Crosses and Sums and the Spokes puzzles are variations of the Spoke Sums puzzle from our math fair website, which is in turn a simpler version of a much older puzzle Henry Ernest Dudeney and/or Boris A. Kordemsky. I don't know who originated the puzzle –– during that era, puzzlers frequently "borrowed" from each other without giving credit.
For more examples of math fair puzzles, visit our SNAP math fair website.
If you are planning to come to this year's workshop and have some favourite math-based puzzles or games, please bring them and share how you have used them in your teaching.






