Three simple ordinal number puzzles

There are two fundamentally different ways that we understand numbers, namely as cardinals and ordinals. When we think of a number as magnitude or size, that's a cardinal number. When order and sequence are the things we want, then we are dealing with ordinal numbers.

In a previous post I related how I handle ordinal numbers more easily than ordered sequences of other things (like the English alphabet). I thought it might be interesting to create a couple of puzzles that deal with ordinal numbers.

Here are three puzzles that are intended for children in the elementary grades, but they can be scaled up to higher levels. The first two are quite new (but I recently discovered a version of the first one in Kordemsky's "Moscow Puzzles".  The third puzzle is one from a small set that I made up over 15 years ago.

Each puzzle asks you to rearrange a set of numbered disks (or tiles) so that they are in numerical order. What makes the puzzles a challenge is that there are restrictions on how you can move the disks.

Swap positions 1

For this puzzle you require five disks numbered 1 though 5. Place them in a line in random order:

The puzzle is to rearrange the numbers so that they are in order:

You cannot just rearrange them any way you want.

Rules:

• You must solve the puzzle in a step by step fashion.
• For each step you must swap the positions of two numbers.

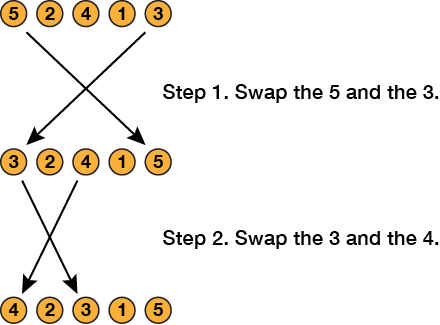
Here are two possible steps for the puzzle above. (Not saying that these steps are part of the solution.)

You always have to swap two numbers. You are not allowed to squeeze one number between two others like this:

Small Spoiler:  (Use your mouse to select the hidden text in the following box.)

With these rules, the solver may soon figure out that you can swap two numbers that are next to each other and successively move a number up and down the line (thereby inventing an algorithm that solves the puzzle).

Swap Positions 2

Let's adjust the rules and make it just a bit more difficult. And because it is more challenging, try it using four numbers instead of five.

New Rules:

• You must solve the puzzle in a step by step fashion.
• For each step you must swap the positions of two numbers.
• The two numbers must have at least one other number between them.

This is what you can and cannot do under the new rules:

Some other modifications are suggested at the end of this post.

The criss-cross puzzle

For this puzzle you will need a grid of squares forming a cross, and three tiles numbered 1, 2, 3 that will fit in the squares of the grid:

Place the tiles in the grid in the order 3-2-1 from left to right. By pushing the tiles within the grid, rearrange them so that they are ordered 1-2-3 from left to right. The tiles must end up in the position shown.

Rules:

• The tiles must always move and stay inside the grid.
• You can push tiles up, down, left, or right as long as you stay inside the grid. You cannot push a tile past, or over, or under another tile.
• If two or more tiles are touching you can push them together at the same time. 
• You cannot separate tiles that are touching by pulling them apart in the same line.

This move is OK. Here, the three tiles have together been pushed to the left.







This move is OK. You can push a tile up or down as long as it stays inside the grid.







But this move is Not OK. You are not allowed to pull tiles apart in the same line if they are touching.





You can also try the puzzle with different starting positions:

Note:  Depending upon the student(s), you might want to prepare them for the puzzle by letting them get familiar with moving the tiles. For example, have them figure out how to solve the following puzzle which only asks them to switch the position of the red tile. It's an interesting puzzle in its own right. The rules for moving the tiles are the same.

Possible modifications

Both swap positions puzzles can be solved for any set of numbers, e.g.,

What if we change the rules so that you are only allowed to swap numbers if they have at least two numbers between them? What other modifications could you make for the puzzle?

You can extend the criss-cross puzzle (to include more tiles) by changing the playing board. Here are two possibilities. The rules remain the same.

Computer science students: Can you write a program that solves these puzzles?

The curious incident of the mathematician at the self-checkout kiosk

We had some produce that had no barcode on the package, so we tapped the [ LOOK UP ITEM ] rectangle on the touch-screen, and it displayed some options for identifying the product:

The product did not have a 4-number code, so the choice was to search for the product alphabetically. For example, if the product was beans you would touch the B - C button which would bring up an array of pictures — Bananas, Basil, Beans (green), Beans (wax), Bread, Brussel Sprouts, etc. (Of course, touching one of these might lead to yet another screen, and so on until you see the exact item you wish to purchase.)

The actual product we wanted was grapes. So indulge me: what button would you touch?

At the kiosk I noticed that there was some hesitation when my wife responded. I wondered if it might be different if she had to choose a number range instead of a letter range. So we both did a quick trial when we got home.

The at-home kiosk task

On the right is a search screen that uses numbers instead of letters.

Here, the problem is to choose the button with the number range that contains the desired number.

Which button would you touch for the number 7?

These is very much the same question with numbers instead of letters. So, why were we able to answer this question much more quickly using numbers? 

Perhaps it is because I have had more practice with numbers — I am a mathematician, after all. But that doesn’t explain why my wife had the same experience — she is not a mathematician — and she also answered more quickly when numbers were used.

When I was a child, we spent a lot of class time learning how to find a word in a dictionary. We learned how to bracket words alphabetically —  and we learned how to put things in order alphabetically, and the teacher made sure we had lots of practice.  We knew the order of the English Alphabet quite intimately. What we did in school was a much more demanding task than selecting the correct screen at a checkout kiosk.

If you have read my previous post (It’s not all snake oil) you know that I have some interest in understanding how the brain (and mind) reacts to numbers.

That post was concerned with cardinal numbers — numbers being used to describe magnitude or size. It is now well established that there is a specialized region of the cortex that reacts to such numbers, and the region seems to be unresponsive to things other than numbers (such as colours, or music, or words that are not tied to numbers).

In the at-home kiosk task, however, we are dealing with ordinal numbers — numbers being used to describe order and sequence.

Recently, cognitive neuroscientists have begun more closely investigating both ordinal numbers and more general (non-numerical) ordered sequences. But the state of affairs is not clear cut. Exactly what happens depends on a large variety of factors.

Even the situation regarding ordinal numbers by themselves appears to be clouded by the fact that numbers represent both magnitude and order. When you are asked "Is 7 between 4 and 11?" do you decide this "immediately" in some sort of a subitizing way, or do you decide by comparing the magnitude of 7 successively to the magnitudes of 4 and 11? The answer seems to be that it depends upon the context, and that affects what regions of the brain are involved.

In particular, I was curious to see if there was a distinction between how the brain deals with the ordered sequence of numbers as opposed to the ordered sequence of the alphabet.

From what I have read the only conclusion I can draw is  "Maybe."

For now, I guess I'll  have to live with the fact that my wife and I are alphabetically challenged.